Research

I’m primarily interested in the fundamental dynamics of the atmosphere. In the meantime, I also enjoy thinking about interesting ways to apply mathematics, physics, and machine learning to natural systems.

1. Dynamical contributions in extra-tropical precipitation extremes

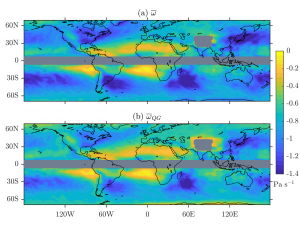
Precipitation extremes are expected to increase under warming. Global-circulation-model (GCM) simulations tell us that the increase in extremes is due to increased water vapor content (thermodynamical contribution), with spatial variances controlled by vertical velocities (dynamical contribution). Therefore, understanding the changes in vertical velocities are important for predicting precipitation extremes in future climates.

My paper in the Journal of Climate looks at the changes in vertical velocities. In our paper, we use the quasi-geostrophic omega equation to decompose these vertical velocity responses into changes in other physical quantities. Our results show that reduction in moist stability and increases in vertical extent are important contributors to the strengthening of vertical velocities.

Fractional changes in (a) pressure velocities associated with precipitation extremes, and (b) quasi-geostrophic pressure velocity calculated from the QG-omega equation.

2. The neural learnability of chaotic dynamics

Neural networks turn out to be a great class of models to learn chaotic dynamics. We found that a 4-neuron classical feedforward neural network (FNN) can be “as chaotic as” the Lorenz-63 system. Furthermore, a 2-neuron FNN is structurally very similar to the Hénon map. It seems that FNNs are structurally similar to chaotic systems. They might be capable of simulating a wide range of low-dimensional chaotic systems using the same functional form and therefore could represent a class of unifying models for these systems.

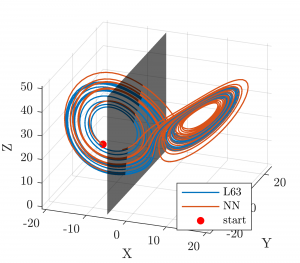
A 5-neuron network trained on Lorenz-63 data points right to the dark-grey divider is able to extrapolate the attractor object to the left of the divider.

See the publication associated with this work at https://doi.org/10.1109/TNNLS.2021.3087497. It is also available on Arxiv: https://arxiv.org/abs/1912.05081. Here’s also my poster presented at AGU fall meeting in 2019.

3. Scaling of tropical precipitation clusters

I’m also interested in the ubiquitous scaling law in precipitation. Specifically, the area of rainfall clusters and total precipitation within a cluster (cluster power) both follow a power-law over a large range of scales. My e-lightning poster at AGU fall meeting, 2019, looks at this phenomenon from a unique perspective: the landscape of the column-water-vapor field.

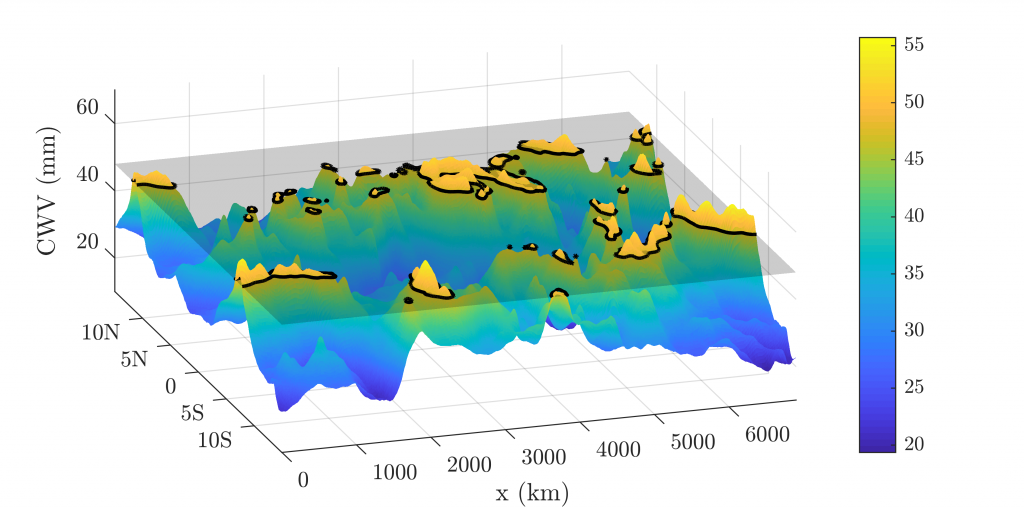
Column-water-vapor landscape with localized islands above a threshold of 48mm. The field is produced from a semi-global cloud-permitting simulation. This threshold is chosen to match the precipitation clusters.

Here’s a link to the e-poster.

4. A simple model for convective organization

More updates to follow!